Basic Computation Models

Turing Machine

• A machine operates on a infinite tape. On this tape are symbols, which the machine can read and write, one at a time, using a tape head. Operation is fully determined by a finite set of elementary instructions.
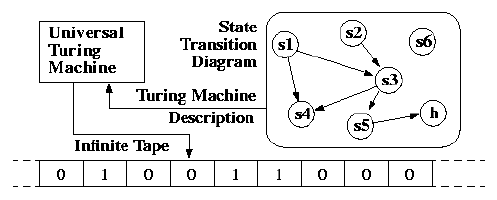
• Despite the model’s simplicity, given any computer algorithm, a Turing machine capable of simulating that algorithm’s logic can be constructed.(Incredibly powerful)

	same program	different program
same data	remains the same	click
different data	click	-

Universal Turing Machine

A Universal Turing Machine can simulate any arbitrary Turing machine on arbitrary input. - A Turing machine computes a certain fixed partial computable function. - A Turing Machine has finite states. Hence, we’re capable of encoding those states. - Programable: by reading both the description of the machine to be simulated as well as the input from its own tape.

Given the appropriate program, a Universal Turing Machine is capable of computing anything that is computable.

Turing Equivalance

2 computers P and Q are called equivalent if P can simulate Q and Q can simulate P.

Turing Complete

A system that can simulate a universal Turing machine is called Turing complete. - Examples: Most programming languages if memory limit is ignored. E.g. C, C++, Python… - Non Turing complete languages: regular languages generated by regular expression, context free grammar

Misc

• Movie: The Imitation Game

Von Neumann Model

Developed based on UTM.

• 4 main components: CU, ALU, memory, I/O
• Programs must be stored in the memory.
• Finite instructions(why?)
• Sequential execution: instructions will be fetched, decoded, and executed one after another, even if there is a jump to previous/following instructions.
  • e.g.
    1. jump to 4
    2. add x and y
    3. jump to 2
    4. jump to 2

Questions

1. What’s a Turing Machine?
2. Is a calculator Turing complete? Give an explaination.
3. Explain the Von Neumann Model.